Does the N64 joystick really allow 360 degrees of control?

One thing I keep on hearing time and time again is that the Nintendo 64 controller was revolutionary because the analogue joystick allows for 360 degrees of control compared to the 8 directions of the classical D-Pad. This is true, it meant for much smoother control in three dimensions and has been a standard for controllers ever since.
But then I got wondering… Does it really allow for 360 degrees, or is that just a figure of speech? Let’s find out.
How the N64 controller reads input
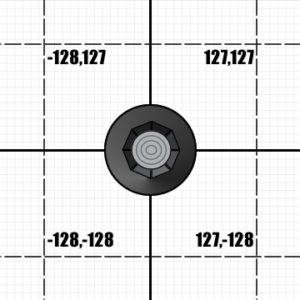
The Nintendo 64 controller feeds the console a 32-bit integer which represents the current buttons pressed, along with the joystick’s inclination. The buttons occupy 16 of those bits (though two aren’t used since the N64 only has 14 buttons). The joystick input is represented by two 8-bit integers that show how much incline there is on the x-axis and y-axis.
typedef struct {
u16 button;
s8 stick_x;
s8 stick_y;
u8 errno;
} OSContPad;
The range of -128 to 127 is only in theory though; those are just upper and lower limits. According to the N64 developer documentation:
Control Stick resolution differs from Controller to Controller. Moreover, as a Controller gets old, the uppermost value that the Control Stick can input can decline. To handle the variation between Control Sticks, we recommend you set the actual usable range to the values shown below.
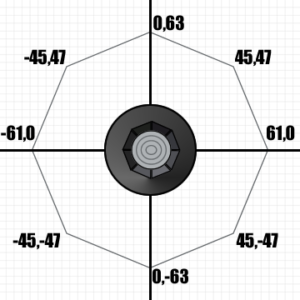
Left/right X axis +/- 61
Up/down Y axis +/- 63
X axis incline +/- 45
Y axis incline +/- 47
This means that when pushing the joystick left or right, the max value used in a program should be 61. Similarly, 63 should be the maximum value for the up and down.
Since the N64 controller joystick resembles an octagon, the maximum diagonal values approximate 70.7% of their maximum horizontal/vertical values.
Actual joysticks max incline
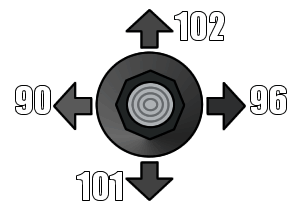
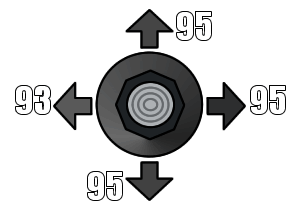
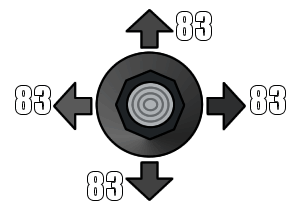
Since there are dozens of joystick types, I decided to try out some real life joysticks with nu1 to find out what the maximum values were for each axis (not counting diagonals).
As you can see, the controller that best approximates the maximum values is the Retro fighters controller. The worn out official controller is the one that barely makes the cut for the minimum requirements. This is the reason why old controllers might not work properly; any more wear on the joystick and it can no longer reach the maximum value for X and Y.
This also comes to show that insensitive controllers like the worn out ones have most of their operational range towards the outer tilts of the controller, while better controllers achieve maximum tilt about 2/3rds of the way out.
The calculation
First let’s do a calculation to find out all the possible angles which the N64 can process based on the maximum range of X and Y (-128 to +127).
The calculation is a simple trigonometry function, using the arc tangent function on the ratio of a specific X and Y coordinate to find the angle theta (θ).
Next, we need to repeat the calculation for every possible coordinate.
There are some coordinates which will repeat themselves because they share the same ratio of X and Y. We’ll exclude them since that will cause duplicate angles on our list.
It’s really as simple as that. Repeat the calculation for each X/Y value and remove duplicates. That’s all there is to it.
The full grid
The simplest calculation is to do the full grid, from -128 to +127. It will be a lot of values, but I’ll get a computer to do the job and save some time. Here’s the PHP script I’ll be using:
<?php
$minx = -128;
$miny = -128;
$maxx = 127;
$maxy = 127;
$values = array();
for ($x = $minx; $x <= $maxx; $x++){
for ($y = $miny; $y <= $maxy; $y++){ $val = $x != 0 ? atan($y/$x) : acos(2); if (is_nan($val)){ $val = pi()/2*($y!=0?$y/abs($y):1); } $val = $val/pi()*180; $val += 90; $val = $x >= 0 ? $val : $val + 180;
if (!in_array($val,$values)){
$values[] = $val;
}
}
}
asort($values);
$total = 0;
foreach ($values as $v){
echo $v."
";
$total++;
}
echo "Total: $total.";
It’s fairly straight forward. The script scans through every possible coordinate and calculates the joystick’s angle. It also handles some exceptions, to avoid division by zero and the like.
The result of the script is amazingly big. There are a total of 39920 possible angles when using the full range of a controller’s input. Here’s a sample of the beginning and to give you an idea of what I’m talking about:
0 0.44761417086055 0.45113854678728 0.45471886169314 0.45835645800042 0.46205272143077 0.46580908276499 0.46962701968964 0.47350805873492 0.47745377730958 0.48146580583834 0.48554583000814 0.48969559312923 0.49391689861875 0.49821161261363 0.50258166672101 0.50702906091477 0.51155586658705 0.51616422976484 0.52085637450195 0.52563460645761 0.53050131667381 0.53545898556453 0.54051018713068 0.54565759341571 0.55090397921856 0.55625222708066 0.56170533256655 0.56726640985794 0.57293869768347 0.57872556560775 0.58463052070518 0.59065721464667 0.59680945122918 0.60309119438053 0.60950657667519 0.61605990839924 0.62275568720632 0.62959860841026 0.63659357596349 0.64374571417538 0.65106038022948 0.6585431775636 0.66619997018314 0.67403689798451 0.68206039317265 0.69027719786507 0.69869438298348 0.70731936854426 0.71615994547041 0.72522429905925 0.73452103425481 0.74405920288869 0.75384833307076 0.76389846092999 0.77422016492805 0.78482460299189 0.79572355273926 0.80692945510236 0.81845546168861 0.83031548625802 0.8425242607404 0.85509739626671 0.86805144974554 0.88140399658214 0.89517371021107 0.90222116153015 0.90938044919913 0.91665425638529 0.92404535277271 0.93155659807748 0.93919094573558 0.94695144677347 0.95484125387217 0.96286362563622 0.97102193107916 0.97931965433948 0.98776039963981 0.99634789650491 1.0050860052542 1.0139787227853 1.0230301886678 1.0322446915657 1.04162667601 1.0511807495437 1.0609116902642 1.070824454787 1.0809241866607 1.0912162252626 1.1017061152064 1.1123996162978 1.1233027140754 1.134421630977 1.1457628381751 1.1573330681295 1.1691393279074 1.1811889133266 1.193489423982 1.20604877922 1.2188752351313 1.2319774026397 1.2453642667683 1.2590452071753 1.2730300200567 1.287328941525 1.3019526725789 1.3169124057933 1.3322198538696 1.3426240265378 1.3478872801986 1.3531919537797 1.3639275316029 1.3748347805694 1.3803540734444 1.3859178508122 1.3971810272964 1.4086287353385 1.4144232114022 1.4202655463991 1.4320961841646 1.4441255309358 1.4502162909334 1.4563586343397 1.4688007143858 1.4814571708871 1.4878675288278 1.4943335912665 1.507435758775 1.5207696611438 1.5275254422129 1.5343414997008 1.548157698978 1.5622249168424 1.569354804749 1.5765500551837 1.5911402711946 1.6060029892822 1.6135389328812 1.6211459136534 1.6365770416167 1.6523046776513 1.6602823689828 1.6683374482933 1.6846843178963 1.7013546053261 1.7098140441415 1.7183580016555 1.7357045889284 1.7534048600715 1.7623910236605 1.7714697400341 1.7899106082461 1.8039951162006 1.8087393224921 1.8183029644518 1.827968244305 1.832839505942 1.8476102659946 1.8626209493067 1.8676788394342 1.8778774472854 1.8881880067409 1.8933858457463 1.9091524329964 1.9251837083231 1.930587441167 1.9414863909144 1.9525090493996 1.958067429234 1.974934010882 1.9920935729664 1.9978798564767 2.0095538130211 2.021364940356 ... 358.00212014352 358.00790642703 358.02506598912 358.04193257077 358.0474909506 358.05851360909 358.06941255883 358.07481629168 358.090847567 358.10661415425 358.11181199326 358.12212255271 358.13232116057 358.13737905069 358.15238973401 358.16716049406 358.1720317557 358.18169703555 358.19126067751 358.1960048838 358.21008939175 358.22853025997 358.23760897634 358.24659513993 358.26429541107 358.28164199834 358.29018595586 358.29864539467 358.3153156821 358.33166255171 358.33971763102 358.34769532235 358.36342295838 358.37885408635 358.38646106712 358.39399701072 358.40885972881 358.42344994482 358.43064519525 358.43777508316 358.45184230102 358.4656585003 358.47247455779 358.47923033886 358.49256424123 358.50566640873 358.51213247117 358.51854282911 358.53119928561 358.54364136566 358.54978370907 358.55587446906 358.56790381584 358.5797344536 358.5855767886 358.59137126466 358.6028189727 358.61408214919 358.61964592656 358.62516521943 358.6360724684 358.64680804622 358.6521127198 358.65737597346 358.66778014613 358.68308759421 358.69804732742 358.71267105847 358.72696997994 358.74095479282 358.75463573323 358.76802259736 358.78112476487 358.79395122078 358.80651057602 358.81881108667 358.83086067209 358.84266693187 358.85423716182 358.86557836902 358.87669728592 358.8876003837 358.89829388479 358.90878377474 358.91907581334 358.92917554521 358.93908830974 358.94881925046 358.95837332399 358.96775530843 358.97696981133 358.98602127721 358.99491399475 359.0036521035 359.01223960036 359.02068034566 359.02897806892 359.03713637436 359.04515874613 359.05304855323 359.06080905426 359.06844340192 359.07595464723 359.08334574361 359.0906195508 359.09777883847 359.10482628979 359.11859600342 359.13194855025 359.14490260373 359.15747573926 359.16968451374 359.18154453831 359.1930705449 359.20427644726 359.21517539701 359.22577983507 359.23610153907 359.24615166693 359.25594079711 359.26547896575 359.27477570094 359.28384005453 359.29268063146 359.30130561702 359.30972280213 359.31793960683 359.32596310202 359.33380002982 359.34145682244 359.34893961977 359.35625428582 359.36340642404 359.37040139159 359.37724431279 359.3839400916 359.39049342332 359.39690880562 359.40319054877 359.40934278535 359.41536947929 359.42127443439 359.42706130232 359.43273359014 359.43829466743 359.44374777292 359.44909602078 359.45434240658 359.45948981287 359.46454101444 359.46949868333 359.47436539354 359.4791436255 359.48383577024 359.48844413341 359.49297093909 359.49741833328 359.50178838739 359.50608310138 359.51030440687 359.51445416999 359.51853419416 359.52254622269 359.52649194127 359.53037298031 359.53419091724 359.53794727857 359.541643542 359.54528113831 359.54886145321 359.55238582914
So in this case, the N64 controller does technically have input for more than 360 degrees. In fact, it averages out to over 100 unique results for each available degree.
Adapting the calculation for expected input
Since the Nintendo 64 controller joystick isn’t perfect, games have to put practical limits on the maximum X and Y values, as mentioned before. This would result in a limit diagram that looks something like this:
This means that we’re going to have to get a bit more creative with our calculation, given that it has an octagon shape. In order to do this, we’re going to need to do two things:
- Reduce the range from -61 to +61 on the x-axis and -63 to+63 on the y-axis
- Make it so that only values inside the hexagon are counted.
The first bit is easy, since it only involves changing the initial values. Simply changing the min/max values makes the total angles go down to 9556, or about 25 angles per degree.
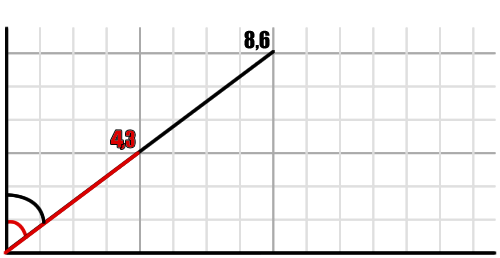
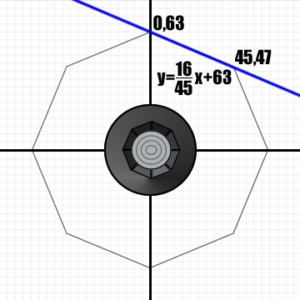
The second part quires a little bit of ingenuity. We need to consider the octagon as a series of eight lines, each of which has a formula. Four of them appear above the x-axis, and another four appear under the x-axis. For the ones above, we want to find points whose y-value is under the line, and vice versa for those under the x-axis. I think it’s a bit more clear if you see it in an image:
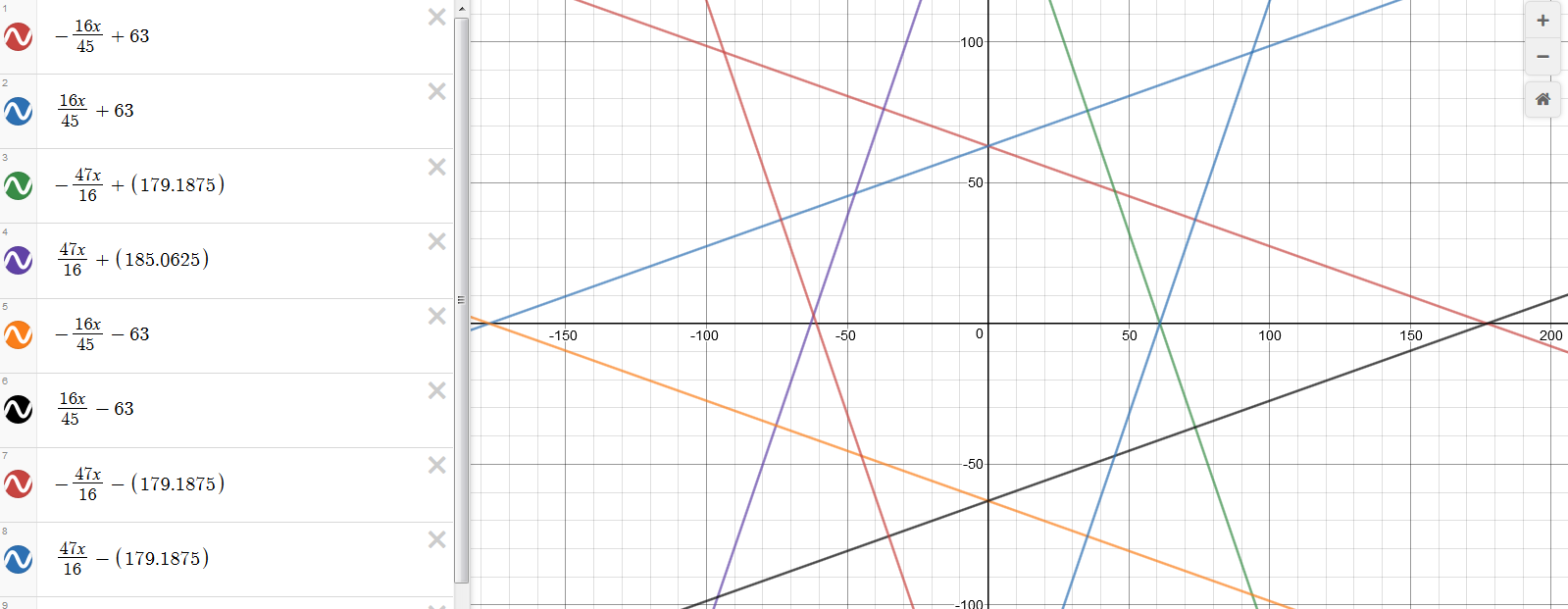
The values in this case have to be below the blue line. If we repeat the calculation for the eight lines, it should tell us whether the point we’re calculating for falls within the octagon. Here are all the equations, for reference (click to enlarge):
Let’s use these equations to add a while bunch of ifs to the code. It’ll make things a lot dirtier, but it’ll make sense once you see it.
for ($x = $minx; $x <= $maxx; $x++){
for ($y = $miny; $y <= $maxy; $y++){
if($y < ($x*16/45)+63) {
if($y < ($x*-16/45)+63) {
if($y < ($x*-47/16)+179.1875) {
if($y < ($x*-47/16)+179.1875) { if($y > ($x*16/45)-63) {
if($y > ($x*-16/45)-63) {
if($y > ($x*-47/16)-179.1875) {
if($y > ($x*-47/16)-179.1875) {
When we run the script we end up with a smaller amount of 7380 possible angles, a whole 2176 less than before. This means that each ‘corner’ we chapped off contained 544 unique angles associated to it.
Conclusion: are there more than 360 degrees?
So after doing all those calculations, we ended up with three values:
- 39920 possible angles if you consider the full range of values for -127 to +128. These are for all the possible inputs considering the limitations of the controller input format.
- 9556 possible angles for the full range for ±61x and ±63y. Since controllers don’t allow for input all the way to -128/127, these are limitations recommended by the documentation to allow even old worn out controllers to work.
- 7680 possible angles when you take into consideration the octagonal shape of the Nintendo 64 controller.
Even under the most restrictive conditions, you can tell that there are a lot more than 360 degrees. In fact, there are about 21.33 angles per degree.
The only question left is to know whether all of these can be used by the N64 as floating point numbers. I suppose that the only thing that might change is the accuracy of each angle, but since they only really need to be accurate to 5 decimals or so to be unique, it should hold up just fine. If anything, that’s an effort for another day.
You can find files detailing all the individual angles that were calculated here.
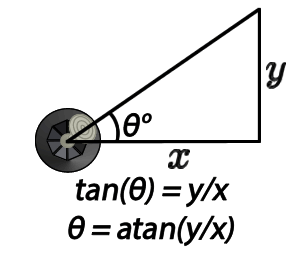


























2 COMMENT
Rodolfo
Thank you so much for this! I find this post very interesting and instructive for people that wonders about the influence of the octogonal shape in the number of angles per degree
Drogie
Really interesting read, thank you!