Gnome Sort

Home » Projects » Sorting Algorithms » Insertion Sorts » Gnome Sort

Gnome Sort is a sorting algorithm that emulates the movement of a Turing machine – having the pointer only be able to move one step at a time.

How Gnome Sort works

Gnome Sort is a variation of Insertion Sort, but with the limitation of not being able to shift the pointer more than one step at a time. This make the visualisation look like there is a gnome moving back and forth along the array carrying over one item at a time.

Example

The array starts with the leftmost item being considered a ‘sorted’ sub-array of size 1. The second item is then picked up and moved leftward until it finds its correct position within the sorted subarray. At this point, Gnome Sort is identical to Insertion sort.

Once this is done, the elements are compared rightwards until an element is found that is out of order. This will eventually put the pointer at the next unsorted element at which point we can repeat the cycle.

The entire list is sorted when the rightward crawl overcomes the length of the array.

Visualisation

TBD

Time complexity

Gnome Sort uses comparisons and swaps to sort the array

Comparisons

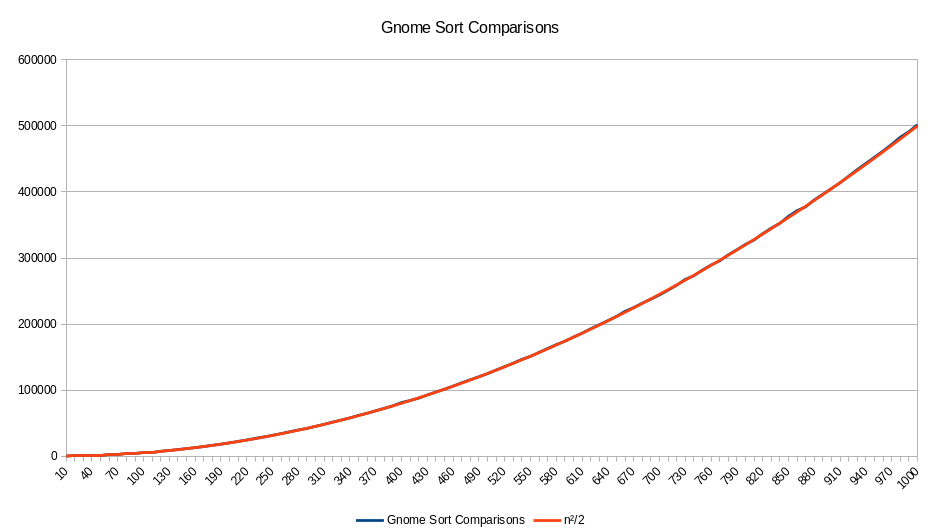
The time complexity for comparisons is n²/2, which makes sense since each step takes twice as long as Insertion Sort.

Swaps

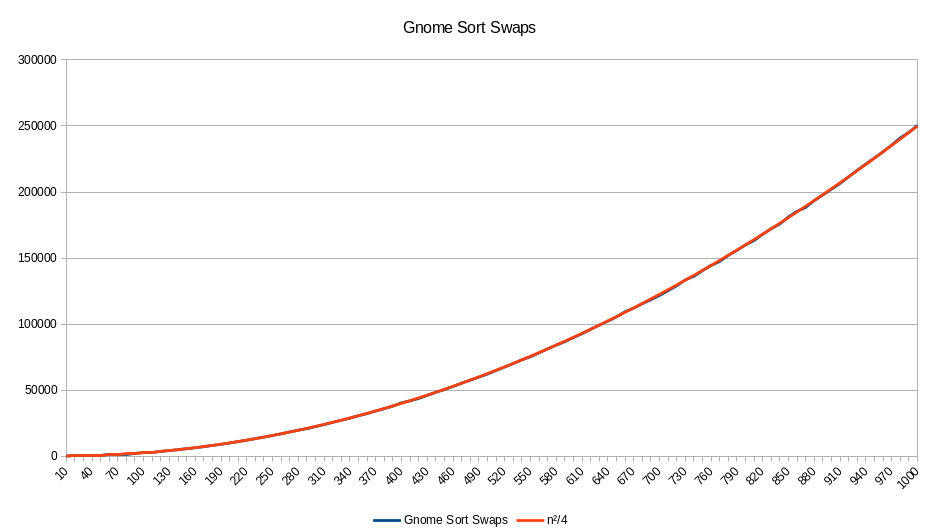
Swaps are on the same order as well but half as much, n²/4.This is because when the gnome move right, no swaps are taking place.

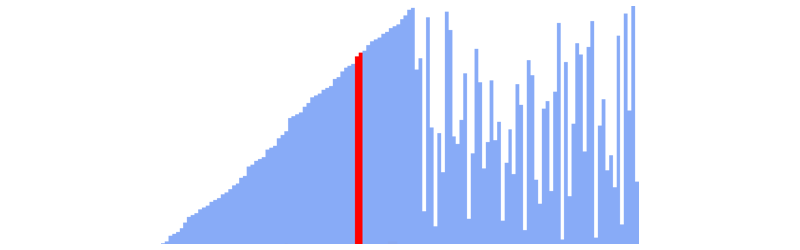
Distribution

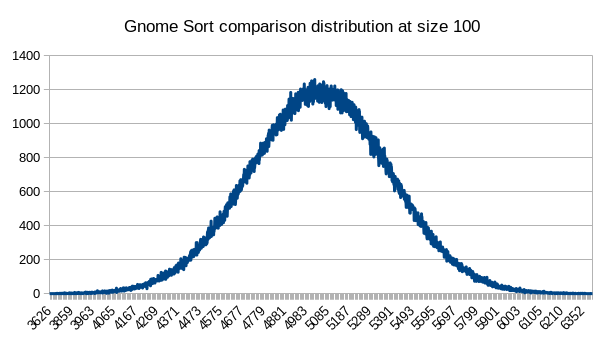
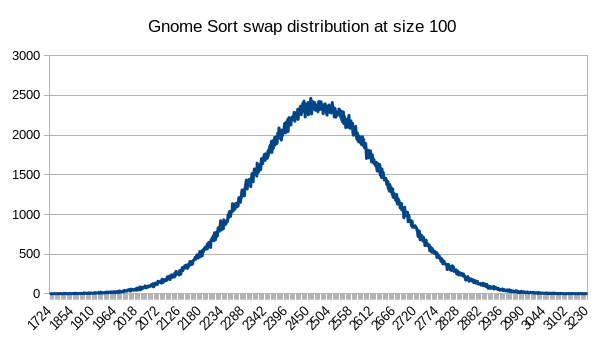
This is how the comparisons and swaps are distributed for this sorting algorithm of size 100 for 1,000,000 sorts.

Mode: 5,023
Mean: 5,046
Std dev: 335
Max: 6,622
Min: 3,482

Mode: 2,457
Mean: 2,475
Std dev: 167
Max: 3,264
Min: 1,692

These distributions aren’t anything out of the ordinary. Just two normal distributions.

C code

void gnome_sort(int *p, int len) {
	int i = 1;
	while (i < len) {
		if (i == 0) {
			// Reached left end, move right and skip
			i++;
			continue;
		} else if (is_greater_than_p(&p[i-1], &p[i]) && i != len) {
			// Swap pots and move leftwards
			swap(&p[i], &p[i-1]);
			i--;
		} else {
			// Move rightwards
			i++;
		}
	}
}