Insertion Sort

Home » Projects » Sorting Algorithms » Insertion Sorts » Insertion Sort

Insertion Sort is one of the simplest sorting algorithms. All it does is move each element and move it leftward until it finds an element that is lower than itself.

How Insertion Sort works

The sorting algorithm starts by declaring the first item in the array as a sorted sub-array. It then takes the second item, adds it to the sub-array and moves it left until the sub-array is sorted again.

This process continues for every item in the array until the sub-array includes all items in the array.

Example

Consider a half-sorted array like this. It is divided into sorted and non-sorted items.

[1, 2, 4, 7, 8, 3, 0, 6, 5, 9]
[1, 2, 4, 7, 8][3, 0, 6, 5, 9]

Then we take the first item from the unsorted array (3) and add it to the sorted items.

[1, 2, 4, 7, 8, 3][0, 6, 5, 9]

The three then moves left one step at a time until it reaches the correct position.

[1, 2, 4, 7, 8, 3][0, 6, 5, 9]
[1, 2, 4, 7, 3, 8][0, 6, 5, 9]
[1, 2, 4, 3, 7, 8][0, 6, 5, 9]
[1, 2, 3, 4, 7, 8][0, 6, 5, 9]

The sub-list is now sorted and the next item can now be put in its position.

Visualisation

TBD

Time complexity

Insertion Sort uses comparisons and swaps to sort the array.

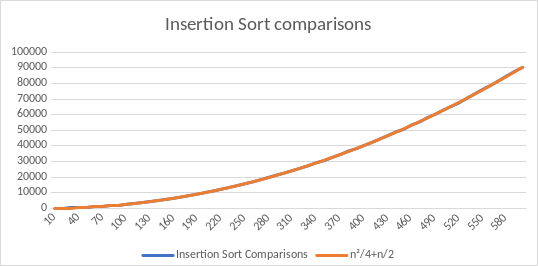
Comparisons

The rate of change for Insertion Sort comparisons is about half as much as Bubble Sort because each element only has to run through half of the sorted sub-array. Bubble Sort on the other hand has to go though the whole unsorted section of the array each time.

It is still a O(n²) algorithm which is pretty slow. Though one big advantage of Insertion Sort is that it has very short code and has very low memory overhead which makes it good for sorting short lists, as a sorter for small subsections of other sorting algorithms or when dealing with very limited resources.

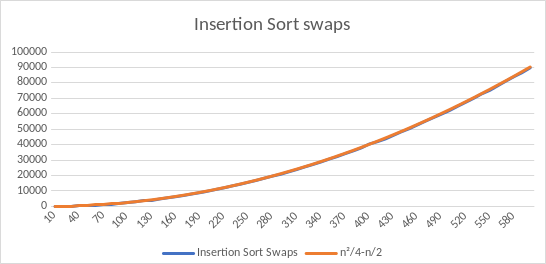
Swaps

Swaps has the exact same distribution as comparisons since every comparison (except the last one in a run) must lead to a swap. This makes it have n fewer swaps than it does comparisons.

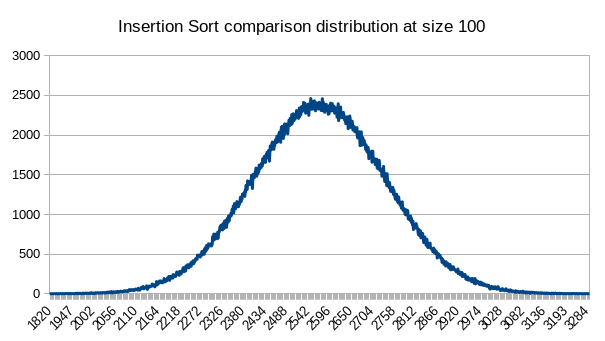
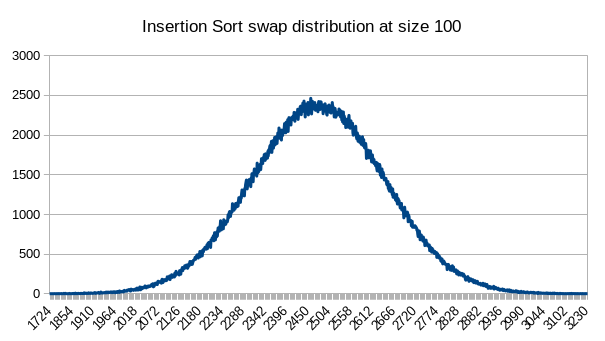
Distribution

This is how the comparisons and swaps are distributed for this sorting algorithm of size 100 for 1,000,000 sorts.

Mode: 2,549
Mean: 2,570
Std dev: 167
Max: 3,357
Min: 1,789

Mode: 2,457
Mean: 2,475
Std dev: 168
Max: 3,264
Min: 1,692

The distributions are pretty much identical because almost every comparison leads to a swap. This makes the only difference is that the numbers for swaps are about 100 lower than those for comparisons.

C code

This is also one of the simplest sorting algorithms out there

void insertion_sort(int *p, int len) {
	int i, j;
	// Loop through unsorted items
	for (i=1; i<len; i++){
		// Loop through the sorted sub-list
		for (j=i; j>0; j--) {
			// Is this one in the wrong position compared to the next one?
			if (is_less_than_p(&p[j], &p[j-1])){
				// Swap them!
				swap(&p[j], &p[j-1]);
			} else {
				// Continue on to the next unsorted item
				break;
			}
		}
	}
}