Quick Sort
Quick Sort is a sorting algorithm that is one of the earliest developed to have reached nlog(n) time while also being able to work in-place.
How Quick Sort works
Quick Sort first starts by picking a pivot. The pivot can be chosen from a specific point (beginning, middle or end) or though a random guess. It then traverses the array and compares every other item to the pivot. If it’s lower, it’s placed on the left; if it’s greater, it goes to the right.
After every item has been sorted compared to the pivot, we guarantee that all items to the left are lower than those on the right, so there is no need to inter-compare them. Instead, we run Quick Sort recursively on the left side and right side until we reach an array of size 1, which is where it returns.
Example
Imagine we have this array:
[1, 9, 8, 5, 3, 0, 4, 6, 2, 7]
We pick a random element as a pivot, say the number 4. Then we compare every number to 4, and place it to the left if it is lower or to the right if it is higher. Eventually, we’ll end up with this:
[1, 3, 0, 2, 4, 9, 8, 5, 6, 7]
Now we know that 4 is in the correct position and everything to the left is lower and everything to the right is higher. Now we perform the Quick Sort algorithm again recursively on these two arrays:
[1, 3, 0, 2] 4 [9, 8, 5, 6, 7]
And on and on until the recursive sizes reach size 1, which is in itself a sorted list.
Visualisation
TBD
Time complexity
Quick Sort uses comparisons and swaps to sort the array.
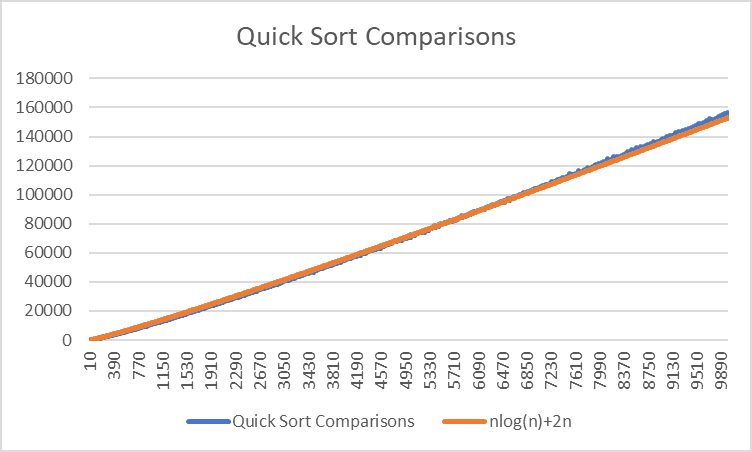
Comparisons
Comparions in Quick Sort follow a pattern bounded by O(nlog(n)), but it doesn’t follow that formula exactly. I tried adding 2n to it, but I have the feeling that it’s not quite right and might diverge at higher numbers
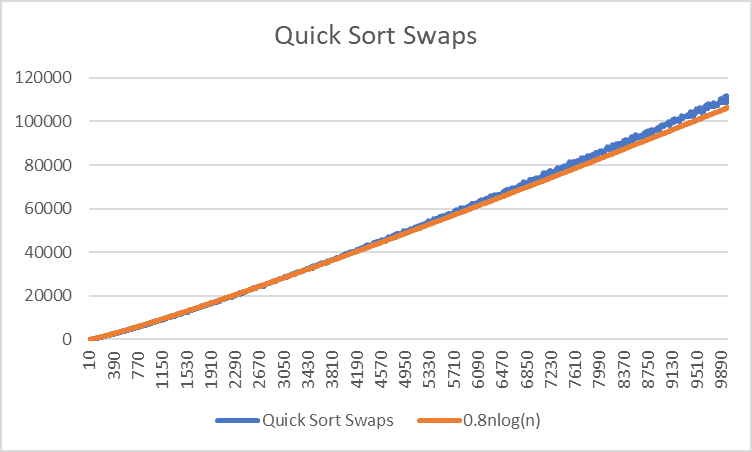
Swaps
Swaps are similarly bounded, but with a lower coefficient.
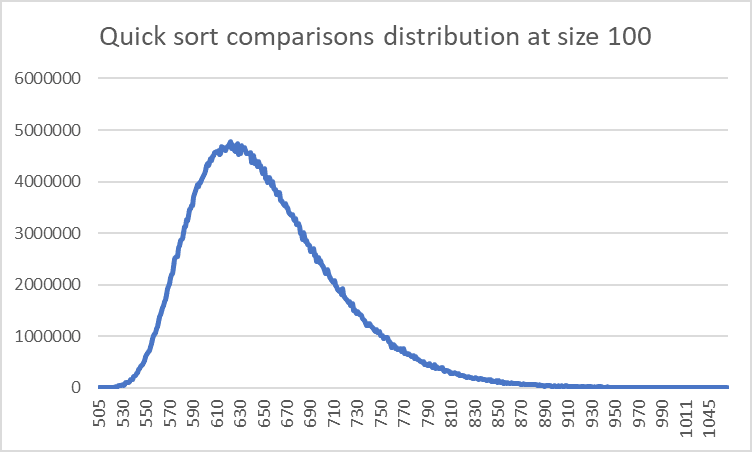
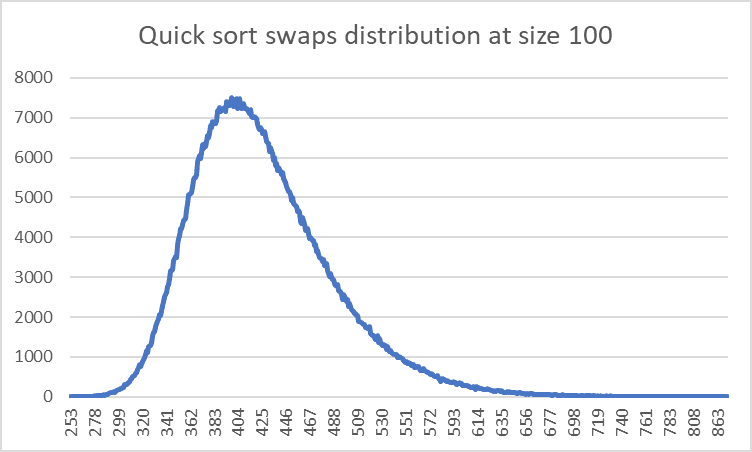
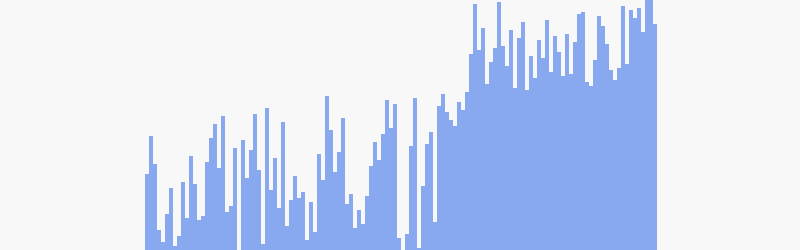
Distribution
This is how the comparisons and swaps are distributed for this sorting algorithm of size 100 for 100,000 sorts.
Mode: 622
Mean: 647
Std dev: 59
Max: 1098
Min: 505
Mode: 398
Mean: 425
Std dev: 61
Max: 901
Min: 253
Both of the distributions are fairly similar, they are a normal distribution that is skewed towards the side.
However what is most interesting about it is what the skews represent for what the best/worst situation that Quick Sort can find itself in.
Theoretically, the worst-case scenario for Quick Sort can end up being equivalent to Bubble Sort. This is because if the pivot you choose is either the maximum or minimum value, it essentially puts all the elements on just one side of the pivot which defeats the point of its divide-and-conquer technique.
The best-case scenario would involve every iteration have the algorithm split it right down the middle. Eventually you’ll get an outcome which is slightly better than the average, with a formula of nlog(n-1), but I could be wrong about that.
C code
void quick_sort(int *p, int len, int level, int pivot) {
int i; // Left side counter
int r=0; // Right (reverse) counter
// Start going through the array upwards
for (i=0; i<len-r;i++) {
if (i < pivot) {
// Picked from the left of the pivot
if (is_less_than(p[i], p[pivot])) {
// It's in the correct position, do nothing
} else {
// It needs to be shifted to the right
swap(&p[i], &p[len-1-r]);
// If we're swapping with the pivot, remember to change the pivot's location
if (len-1-r == pivot) {
pivot = i;
}
r++;
i--;
}
} else if (i == pivot) {
// Is the pivot, do nothing
continue;
} else {
// Picked from the right
if (is_greater_than(p[i], p[pivot])) {
// It's in the correct position, do nothing
} else {
// It needs to be shifted to the left, just before the pivot
if (i > pivot+1) {
// Swap with the one right after the pivot if it is too far away
swap(&p[i], &p[pivot+1]);
}
// It should be right after the pivot now, swap with the pivot
swap(&p[pivot], &p[pivot+1]);
pivot++;
}
}
}
// Call recursively
// Left side
if (pivot > 1) {
quick_sort_recursive(p, pivot, level+1, rand() % pivot);
}
// Right side
if (len-pivot-1 > 1) {
quick_sort_recursive(&p[pivot+1], len-pivot-1, level+1, rand() % (len-pivot-1));
}
}
