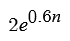Hanoi Sort
Hanoi Sort is an original sorting algorithm that uses the Tower of Hanoi puzzle to very inefficiently sort a list. I first published it on 6 June 2023.
How Hanoi Sort works
The idea behind this algorithm is that it’s a mixture between Selection Sort and the Tower of Hanoi puzzle. The list sorts the first three items normally, but then inserts new items into the sorted array by first moving all lower elements in a tower transfer.
The first three elements are assumed to be placed on each peg at the start of the round, so sorting them is pretty trivial. Just place the middle one on the large one and the small one on top of that. The good news is that in this sorting algorithm, all pegs are equal and can be exchanged as needed so there is no such thing as a ‘left’, ‘middle’ or ‘right’ peg.
Now that we have a sorted sublist, it’s time to add items to it. The next item is picked up and added to an empty peg. Then the Tower of Hanoi is moved from one peg to another like in the normal puzzle, but stops once this new item can fit in the un-moved section of the sorted sublist. Then the new item and the moved portion of the sublist are put back onto the tower using the Tower of Hanoi movement algorithm.
This process is repeated until the entire list is sorted.
Example
Here is a visual example of how adding a new element to the list would look. The algorithm first checks to see if the new element fits on top, and if not it keeps on removing elements Hanoi-style until it finds a place where to place it.
Visualisation
TBD
Time complexity
Hanoi Sort uses comparisons and inserts primarily, and only uses swaps to reverse the array.
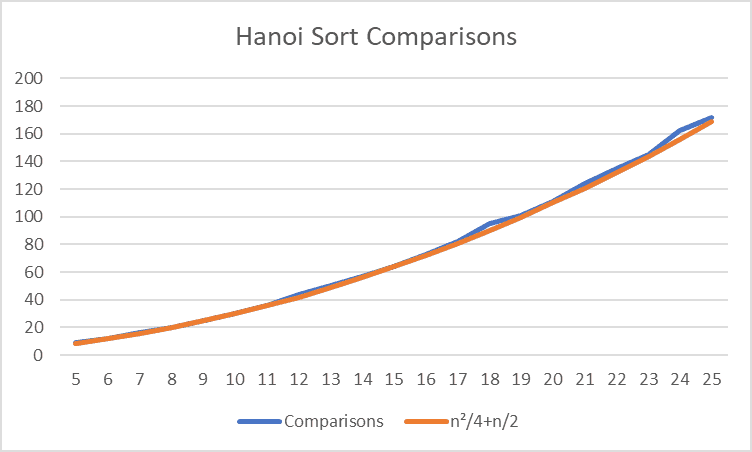
Comparisons
This follows a fairly similar pattern to Insertion Sort, which is O(n2-n)/4). This is likely because Hanoi sort performs comparisons against every item in a pre-sorted list until it find the correct place to put it. The concept is the same, it’s just the method used to ‘insert’ them that changes.
Inserts
Insertions are where it gets interesting. The Tower of Hanoi puzzle is famous for its exponential time complexity because every time you add a new disk, you have to repeat everything done with all the previous disks. For example, moving a 3-disk tower takes 7 steps. But moving a 4-disk tower means that you first need to move the 3 disks on top of it (7 moves), then the 4th disk (1 move) and then the top 3 again (7 moves) for a total of 15 moves. 5 disks would be 31 moves, 6 would be 63 and 7 would require 127 moves.
While that makes it simple to calculate how long it will take to move a particular tower from one peg to another, it’s hard to tell how long each tower is going to take. The size of the sublist on each iteration is going to be [3, 4, 5, 6, …, n] so the size of the Hanoi tower at each insertion is going to be on average sublist/2, and then sublist/2+1 to place it back.
The problem with estimating this is that due to the exponential nature of the Hanoi tower move function, the worst-case scenario (traversing the whole sublist) is much worse than the best case scenario (no traversal needed because the new item is smaller than the rest). For example, a sublist of 10 items, a best case would be just move a tower of 1 (1 move), the median would move a tower of 5 (31 moves x2), and the worst case would move all 10 items (1023 moves x2).
This makes it very difficult to make an approximation formula, based on how it works, so I made a formula that matches the approximate values in the chart by trial and error:
It’s not perfect but it works for now.
Swaps
Hanoi Sort’s swaps re pretty much trivial since it could be done in the correct order to begin with, avoiding swaps altogether. Otherwise it’s a pretty straightforward O(n/2).
Distribution
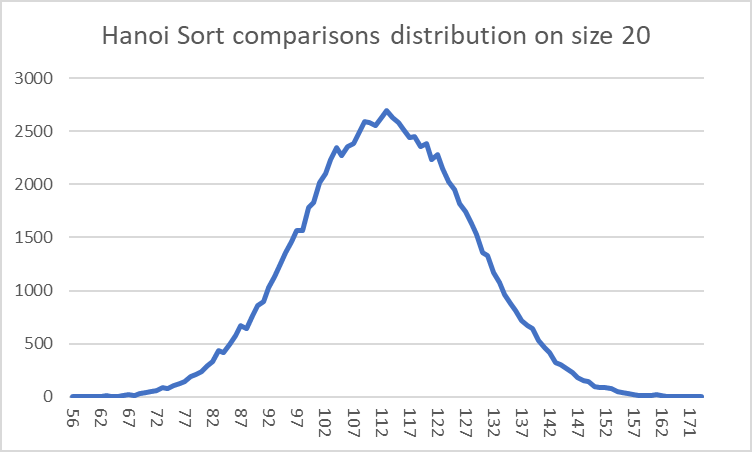
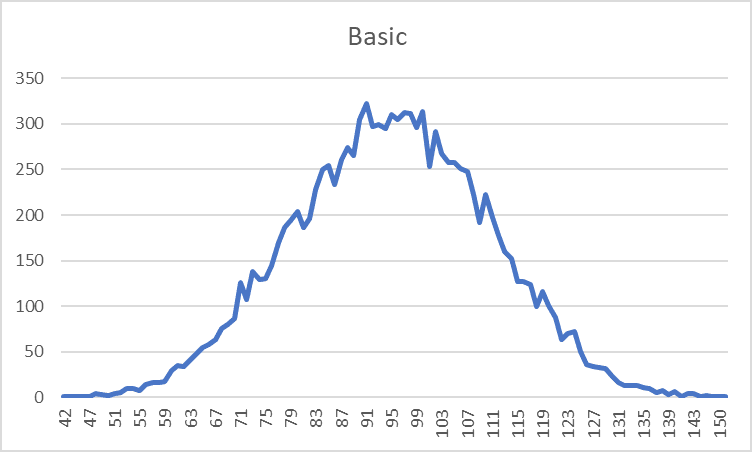
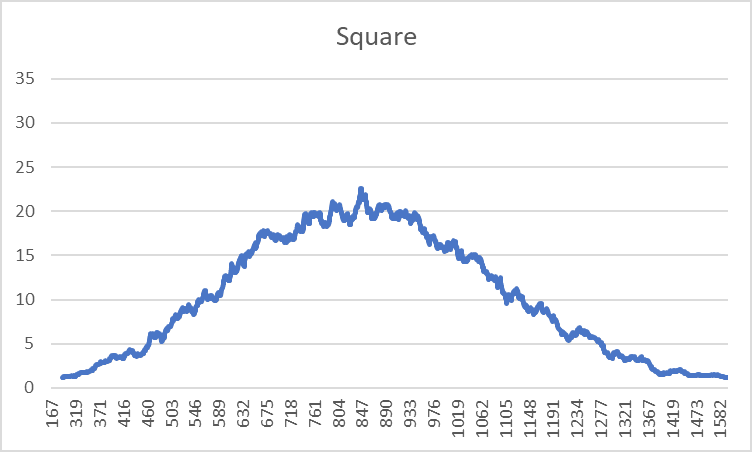
This is how the comparisons and insertions are distributed for this sorting algorithm of size 20 for 100,000 sorts.
Mode: 113
Mean: 113
Std dev: 15
Max: 177
Min: 56
Mode: 4,907
Mean: 258,836
Std dev: 321,264
Max: 1,998,792
Min: 295
Comparisons follow a normal distribution with a mean at the expected time complexity of (n2+n)/4. Pretty simple. The distribution for swaps is even more trivial.
The insertion distribution is more interesting however. As explained in the previous section about the time complexity of the insertions, an unfavourable ordering can have many orders of magnitude more steps than the average (expected) time to completion, greatly distorting the time it takes to complete upwards.
What this means is that we get a very high concentration along the very left while eventually tapering off as the numbers increase.
However what is most interesting is the seemingly random peaks that occur. I find it kind of fascinating because it appears to be a sort of Fourier transformation. If we first look at the most obvious peaks, the last one occurs at around 220 (~1m), the one that is two to the left of it occurs at 219 (~500k) and so on. This is because the most important item to add in is the final item since it will take (on average) the most movements to place correctly.
As for all the other peaks that aren’t on a 2n point, they represent the sum of multiple results. For example, the one that occurs at ~786k is a combination of 219 and 218. Or if the final two items both end up performing 219, you’ll end up with a similar peak to one with 220.
To show this another way, consider these three equations for a sum S where rand() picks a random number from 0 to the parameter:
S1 = rand(1) + rand(2) + rand(3) + … + rand(n)
S2 = rand(1)2 + rand(2)2 + rand(3)2 + … + rand(n)2
S3 = 2rand(1) + 2rand(2) + 2rand(3) + … + 2rand(n)
If we take the result of each S and place it on a graph of 10,000+ attempts, we get these patterns:
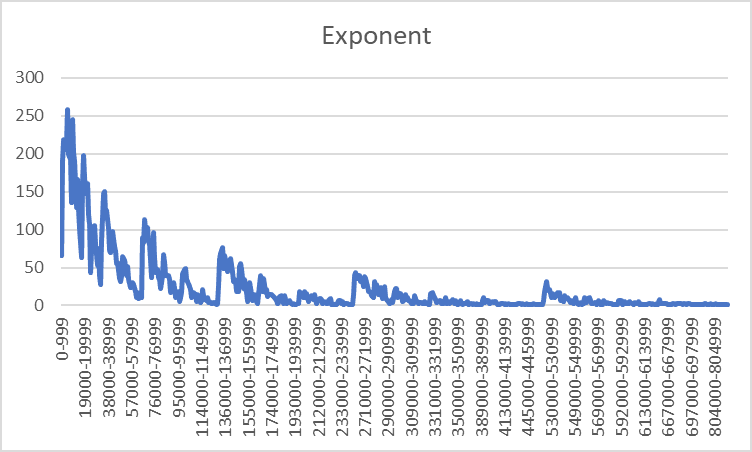
As you can see, summing the numbers in S1 creates a normal distribution. With S2, we also get a normal distribution but flatter (higher stddev) and the median is slightly skew from the mean. When you look at S3, we get a similar pattern to what we got with Hanoi Sort’s insertion distribution.
C code
// Move the top disc from one peg to another
void hanoi_swap(int* p, int* pegs, int source, int target) {
int i; // Loop iterator
int source_index = 0, target_index = 0; // Indices for the tip of the peg
int temp = 0; // Temp variable
// Loop through pegs
for (i=0; i<HANOI_PEGS; i++) {
// Temp is holding the current cumulative size of each peg
temp += pegs[i];
// If we've reached the source peg, keep track of its index in *p
if (source == i) {
source_index = temp-1;
// If we've reached the target peg, keep track of its index in *p
} else if (target == i) {
target_index = source > target ? temp : temp-1;
// Min out at zero to avoid negative indices
target_index = target_index <= 0 ? 0 : target_index;
}
}
// Don't need peg sizes anymore, let's do the resizing
pegs[source]--;
pegs[target]++;
// Temp is now the value of the element we're moving to another peg
temp = p[source_index];
// Compare the indices to determine whether we're moving left or right
// Start by shifting all items one by one
if (source_index > target_index) {
// We're moving leftward
for (i=source_index; i>target_index; i--) {
p[i] = p[i-1];
}
} else {
// We're moving rightward
for (i=source_index; i<target_index; i++) {
p[i] = p[i+1];
}
}
// Finally insert the temp value back in
insert(&p[target_index], temp);
}
// Move an entire stack over to another peg
void move_tower (int* p, int* pegs, int from, int to, int aux, int height) {
if (height == 0) {
return;
}
move_tower(p, pegs, from, aux, to, height-1);
hanoi_swap(p, pegs, from, to);
move_tower(p, pegs, aux, to, from, height-1);
}
void hanoi_sort(int *p, int len) {
int pegs[HANOI_PEGS] = {1,1,1}; // Array holding the length of each peg
char min, mid, max; // Min / Mid / Max value for initial sort
int i, j; // Loop iterators
unsigned char source_peg=0, target_peg=0; // Used to hold the source/target for the current move_tower()
int disc; // Temp value to hold the disc size being inserted into the structure
// Sort the first three items
if (len <= 1) {
return;
} else if (len == 2) {
if (is_greater_than(p[0], p[1])) {
swap(&p[0], &p[1]);
swap(NULL, NULL);
}
} else {
// Sort three items, one on each peg
min = array_min(p, HANOI_PEGS);
max = array_max(p, HANOI_PEGS);
for (i=0; i<HANOI_PEGS; i++) {
mid = i!=min && i!=max ? i : mid;
}
// Organise the first three discs onto one peg
hanoi_swap(p, pegs, mid, max);
hanoi_swap(p, pegs, min, max);
// Loop through each of the discs that are not on the stack
for (; i<len; i++) {
// Reset the pegs to have the stack be on the leftmost one
// and add a new disc on the rightmost peg
pegs[LEFT_PEG] = i; pegs[MID_PEG] = 0; pegs[RIGHT_PEG] = 1;
disc = p[i];
// Loop through the stack until we reach the correct position for the new disc
for (j=pegs[LEFT_PEG]-1; j>=0; j--) {
// Check if the disc is ready to move back to the main stack
if (is_less_than_or_equal_to(disc, p[pegs[LEFT_PEG]-1])) {
// No need to undo the tower any more, let's move it back.
break;
} else {
// Unveil the next disc
// Alternate the current target peg
target_peg = 1 + (j%2);
source_peg = target_peg ^ 3;
hanoi_swap(p, pegs, 0, target_peg);
move_tower (p, pegs, source_peg, target_peg, 0, pegs[source_peg]-(source_peg==2?1:0));
}
}
// The sublist should be sorted, let's move it back to the first position
if (target_peg % 2) {
// The new disc is on a different peg from the rest of the stack.
// Move it first and then do the rest of the stack.
hanoi_swap(p, pegs, RIGHT_PEG, LEFT_PEG);
move_tower(p, pegs, MID_PEG, LEFT_PEG, RIGHT_PEG, pegs[MID_PEG]);
} else {
// The new disc is under the stack. Move the whole thing.
move_tower(p, pegs, RIGHT_PEG, LEFT_PEG, MID_PEG, pegs[RIGHT_PEG]);
}
}
}
// Reverse the array
for (i=0; i<len/2; i++) {
swap(&p[i], &p[len-1-i]);
}
}
