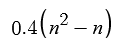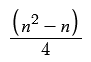Cocktail Sort

Home » Projects » Sorting Algorithms » Exchange Sorts » Cocktail Sort

Cocktail sort is a sorting algorithm that works as a bi-directional Bubble Sort. It has this name because it resembles a cocktail shaker in its visualisation.

How Cocktail Sort works

It follows the same procedure as Bubble Sort in that it scan adjacent pairs of items and swaps them if they are out of order. The main difference is that after finishing a run upwards through the array, it continues downwards until it reaches the bottom of the array, creating an increasingly large sorted area on both the top and bottom.

The sorting continues up and down until the sorted areas meet in the middle. There is also a sortedness checker that checks if the unsorted areas are actually already sorted.

Example

In an array of, say, 10 items, the first run will leave one sorted item on top and another on the bottom. The second run will have two items on top and bottom.

This means that each loop sorts two items at a time, but takes twice as long since the array needs to be traversed in both directions.

Visualisation

TBD

Time complexity

Cocktail Sort uses comparisons and swaps to sort the array.

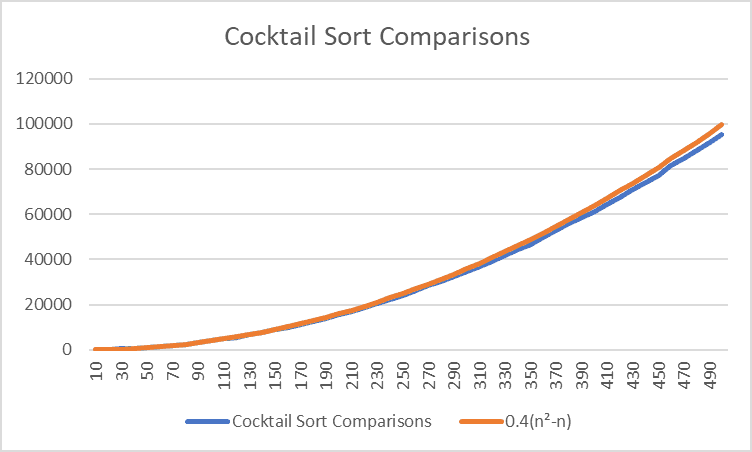
Comparisons

Compared to Bubble Sort, it does work a little bit faster. This is primarily because it can save time with the P value in two directions rather than with just one.

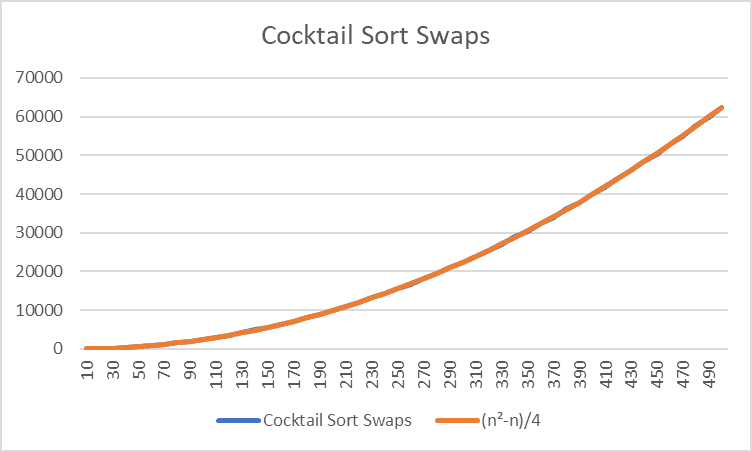
Swaps

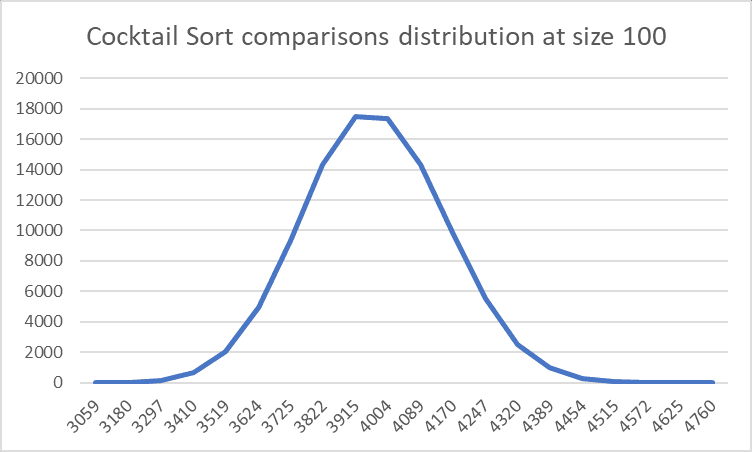
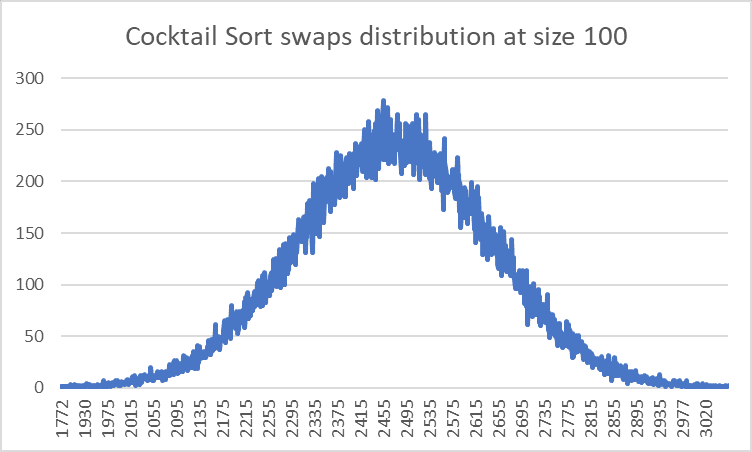
Distribution

This is how the comparisons and swaps are distributed for this sorting algorithm of size 100 for 100,000 sorts.

Mode: 3,915
Mean: 3,957
Std dev: 195
Max: 4,760
Min: 3,059

Mode: 2,455
Mean: 2,474
Std dev: 167
Max: 3,184
Min: 1,772

They’re both normal distributions. The only big difference is that comparisons have one of 20 discrete values while swaps is a bit more continuous, allowing for more randomness.

C code

void cocktail_sort(int *p, int len) {
	// Declarations
	int i, j, done;

	// Loop through runs
	for (i=0; i<len/2; i++){
		done = 1;
		// Bubblesort rightward
		for (j=i; j<len-i-1; j++) {
			if (is_greater_than(&p[j], &p[j+1])){
				// Swap them!
				swap(&p[j], &p[j+1]);
				done = 0;
			}
		}
		// Bubblesort leftward
		for (j=len-i-2; j>i; j--) {
			if (is_greater_than(&p[j-1], &p[j])){
				// Swap them!
				swap(&p[j], &p[j-1]);
				done = 0;
			}
		}
		// If nothing was swapped in this run, then end it
		if (done) {
			return;
		}
	}
}