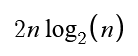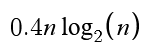Comb Sort
Comb Sort is another simple sorting algorithm, kind of like a combination of Shell Sort and Bubble Sort. It’s named that way either because the gap ‘combs’ through the input array, or because an almost-sorted list looks kind of like a comb.
How Comb Sort works
Similar to Bubble Sort, Comb Sort is an algorithm where you compare two items and swap them if they are out of order. The difference is that Comb sort doesn’t compare adjacent element exclusively, but rather has a gap between the two. The gap starts at n elements long, but is then reduced by a factor of 1.3 after each passthrough of the array.
Example
For example on an array of 100 elements, you’ll first start with a gap of 100 (which will only do 0 or 1 comparison). The next run will have a gap of 76, which will compare the top 24 items with the bottom 24 items. The next gap will be 58, then 44, then 34, 26, 20, 15, 12, 9, 7, 5, 4, 3, 2, and finally 1.
Visualisation
TBD
Time complexity
Comb Sort uses comparisons and swaps, but no inserts or data reads.
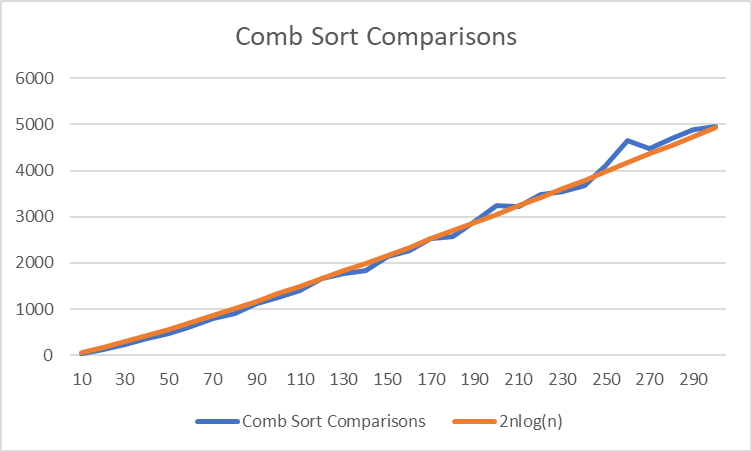
Comparisons
Comb Sort is a lot more volatile than Bubble Sort so it’s a bit harder to get an accurate best-fit formula, but it does seem to be very close to this:
This makes Comb Sort a much better alternative, but still quite slow in comparison to other nlog(n) algorithms.
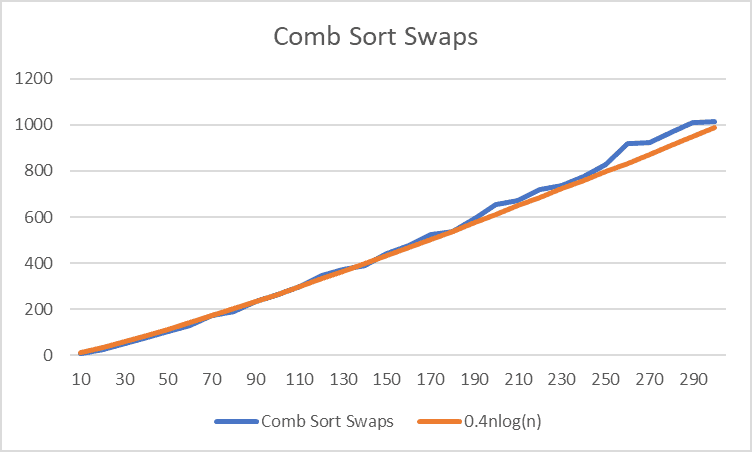
Swaps
Swaps follow a very similar pattern to comparisons, but with a smaller gradient coefficient.
This means that it only performs a swap every ~4 comparisons, making it more efficient in terms of the ‘swap efficiency’ than bubble sort.
Distribution
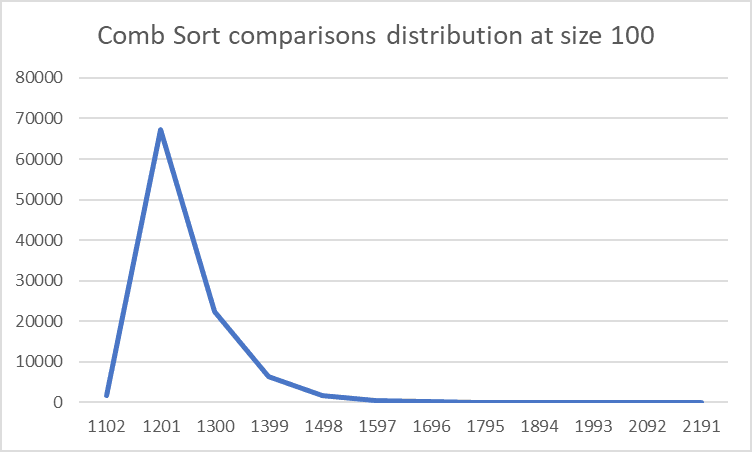
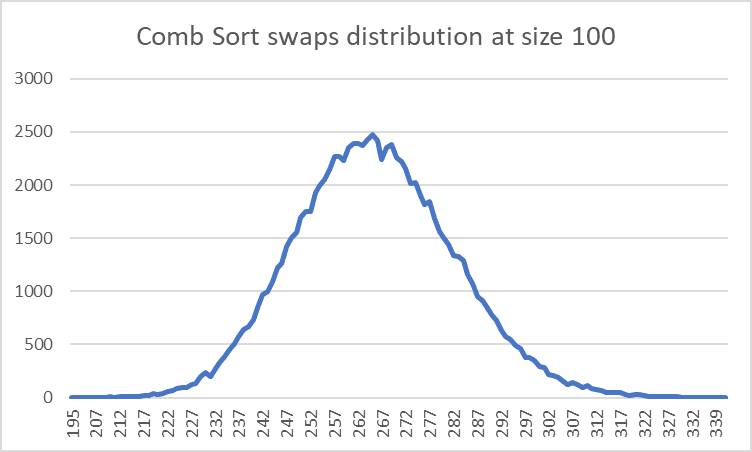
This is how the comparisons and swaps are distributed for this sorting algorithm of size 100 for 100,000 sorts.
Mode: 1,201
Mean: 1,241
Std dev: 76
Max: 2,191
Min: 1,102
Mode: 265
Mean: 265
Std dev: 16.6
Max: 342
Min: 195
From the comparison graph, we can see that there are very few (only 12) output possibilities, with most of them concentrated on the lower end.
The swap graph is a fairly standard normal distribution.
There are cases where it would take longer if the array is in a progressively more reverse order and would need to make additional runs through. A worst-case run of Comb Sort (a reversed array as input) would have 3,790 comparisons and 354 swaps.
C code
void comb_sort(int *p, int len) {
int i; // Loop iterator
char sorted = 0; // Sorted flag
const float shrink = 1.3; // Shrink factor
int gap = len; // Gap between items
// Loop through until list is sorted
while (!sorted) {
// Decrease gap by a bit each time
gap = (int)(gap/shrink);
if (gap <= 1) {
sorted = 1;
gap = 1;
}
// Compare all items with gap distance between them
for (i=0; i<len-gap; i++) {
// Compare and swap
if (is_greater_than_p(&p[i], &p[i+gap])) {
swap(&p[i], &p[i+gap]);
// We swapped something, set it to unsorted.
sorted = 0;
}
}
}
}
