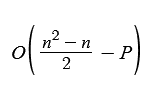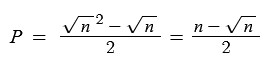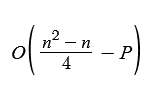Bubble Sort
Bubble Sort is the quintessential sorting algorithm. It’s the kind of function that most people would think about when first trying to sort a list. It also happens to be one of the worst ways to do so without actively trying to make an inefficient algorithm.
I has this name because through every iteration, the selected item grows and floats to the top, kind of like how a bubble does in water.
How Bubble Sort works
In order to sort a list using Bubble Sort, you need to traverse the array, comparing adjacent elements and swapping them if they are out of order. This will ensure that the highest element is always at the very end of the array. The process is then repeated (excluding this highest element) until all elements have been checked.
There is also a checker that checks if there have been any swaps in the current run. This helps a bit by skipping some runs if the tail end is already sorted. It also helps reduce the time complexity from O(n2) to O(n) when the list is pre-sorted.
Example
If we consider an array of 100 elements, we can start at the very left. Compare items at position 0 and 1; if 0 is greater, swap them, otherwise do nothing. Then compare position 1 and 2, then 2 and 3 etc. Once we reach 98 and 99, we know that the largest element exists in position 99.
Now the process is repeated from the beginning which puts the next highest (or equal) number in position 98 and so on until the array is completely sorted. If an antire run is completed without any swaps, the list is considered sorted and the function returns.
Visualisation
TBD
Time complexity
Bubble Sort uses comparisons and swaps, but no inserts or data reads.
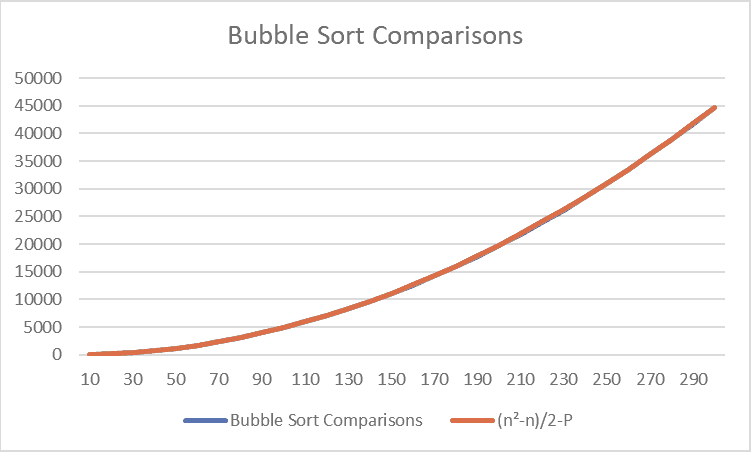
Comparisons
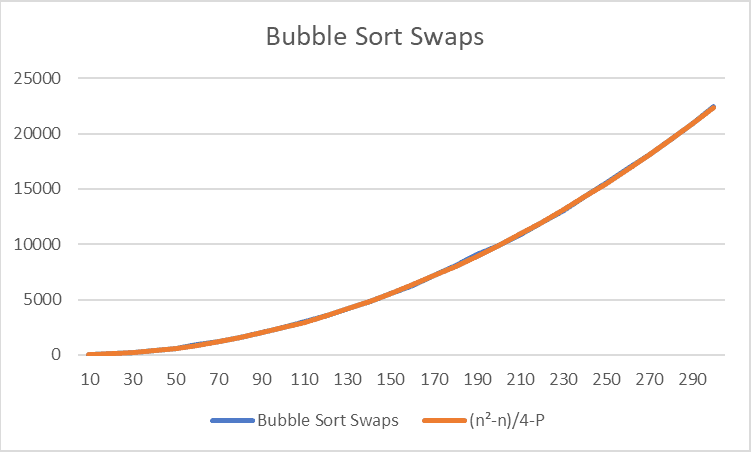
The straightforward formula for the comparison complexity is fairly simple:
Now to explain: The left side indicates how long it would take to complete Bubble Sort if it was just the two loops, but the P refers to the comparisons that have been skipped because of the sortedness check.
Calculating P
P itself is a bit harder to calculate since it varies based on the initial position of the array. I found that it generally tends to skip sqrt(n) iterations as its statistical mode. It does look like a normal distribution, but skewed rightwards so the mean is always going to be greater than the calculated mode.
This makes the formula for the mode of P as follows:
Swaps
And the formula for swaps is:
As you can see, the time complexity for Bubble Sort swaps is about half of its comparisons, meaning that each comparison has an approximate 50% chance of causing a swap to occur.
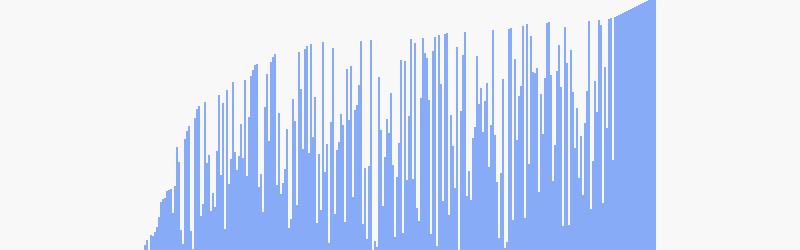
Distribution
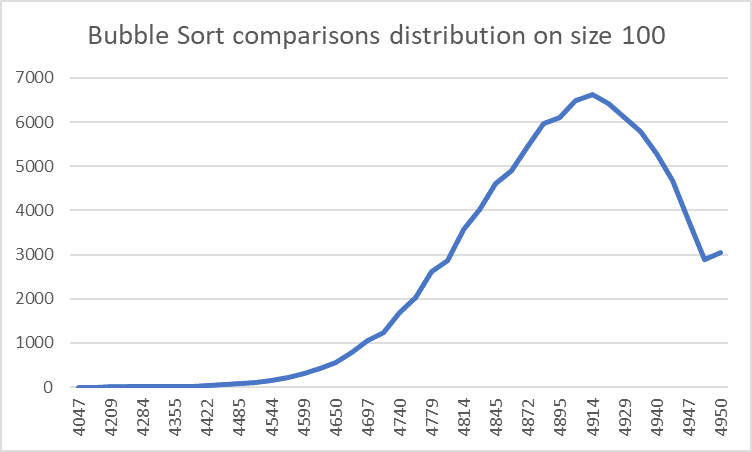
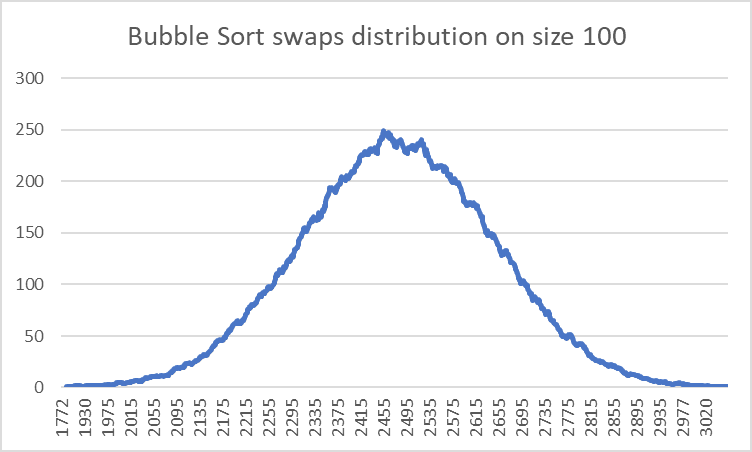
This is how the comparisons and swaps are distributed for a Bubble Sort of size 100 for 100,000 sorts.
Mode: 4,914
Mean: 4,878
Std dev: 75
Max: 4,950
Min: 4,047
Mean/mode: 2,474
Std dev: 167
Max: 3,184
Min: 1,772
As we can see from the comparisons, there is a max value of 4,914 which corresponds to the estimated comparisons from the formula.
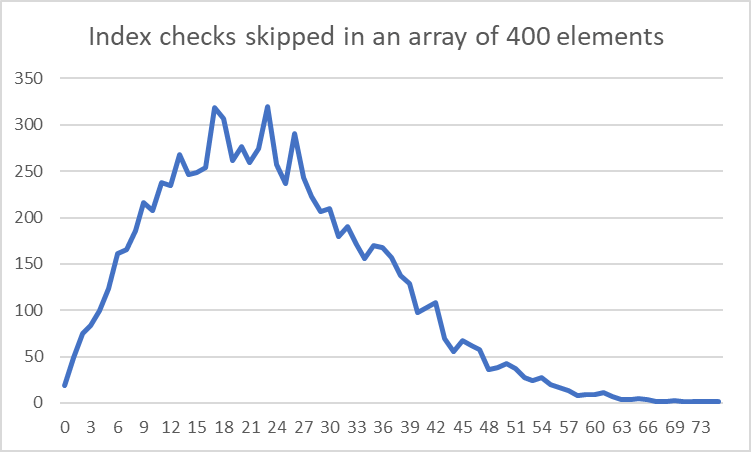
Where it gets interesting is when we take P into account. The rightmost value (no time savings) is almost the same as only one element saved since it’s essentially a 50/50 chance of getting one or the other. The likelihood of several runthroughs of saving is higher however because the Bubble Sort algorithm not only stacks the highest elements towards the right, but also the indirectly the lowest elements towards the left.
In this example, you can see how the leftmost ~3 elements are already sorted even though we still have ~20 elements left to sort.
On the other hand, swaps have a normal distribution
C code
Here is an overly-annotated version of Bubble Sort in C:
void bubble_sort(int *p, int len) {
// Initialise variables
int i, j; // Loop iterators
char sorted = 0; // Sorted flag
// Loop through each run
for (i=0; i<len && !sorted; i++){
// Set the sorted flag to 1
sorted = 1;
// Loop through each pair of elements
for (j=0; j<len-i-1; j++) {
// Are they out of order?
if (is_greater_than(p[j], p[j+1])){
// Swap them!
swap(&p[j], &p[j+1]);
// Set the sorted flag to 0 so that we don't stop sorting
sorted = 0;
}
}
}
}
