Slow Sort

Home » Projects » Sorting Algorithms » Exchange Sorts » Slow Sort

Slow Sort is an algorithm that was purposely designed to be as slow as possible. It is often described as a multiply-and-surrender algorithm in contrast to the divide-and-conquer method used in nlog(n) algorithms.

It’s one of the few algorithms to have a time complexity on the order of O(2ⁿ), also known as exponential.

How Slow Sort works

Slow Sort works kind of like Bubble Sort in that each run is all about choosing the top element and putting it in place at the right side of the array. In order to do that recursively, it slow sorts the first half and then the right half. The top element of each half is compared in order to find that highest value.

It feels a lot like Merge Sort, except that every time two halves are to be sorted, it recursively checks all sub-elements, leading to a lot of repetition.

Example

Let’s start with a small array like this and try to place the first item:

[1, 0, 4, 2, 3]

It will first split the array into two.

[1, 0] [4, 2, 3]

Since the left half is just two items, the split won’t do anything. It will just go on to compare the two elements and swap if needed.

[0, 1] [4, 2, 3]

Then deal with the right-hand side. First split once to isolate the 4, and then again to compare the 2 and 3. They are in order so nothing happens. Then compare the 4 and 3 (the top elements of the two subarrays) and swap them because they’re out of order.

[0, 1] [4] [2, 3]
[0, 1] [3, 2, 4]

Now compare the top items of both subarrays at the next level up (1 and 4) and we’ll see that the rightmost element is now in the correct position.

[0, 1, 3, 2, 4]

Now repeat the process again with the rest of the items, and do it again until we work our way through the whole array.

[0, 1, 3, 2] [4]

Visualisation

TBD

Time complexity

Slow Sort uses comparisons and inserts primarily, and only uses swaps to reverse the array.

Comparisons

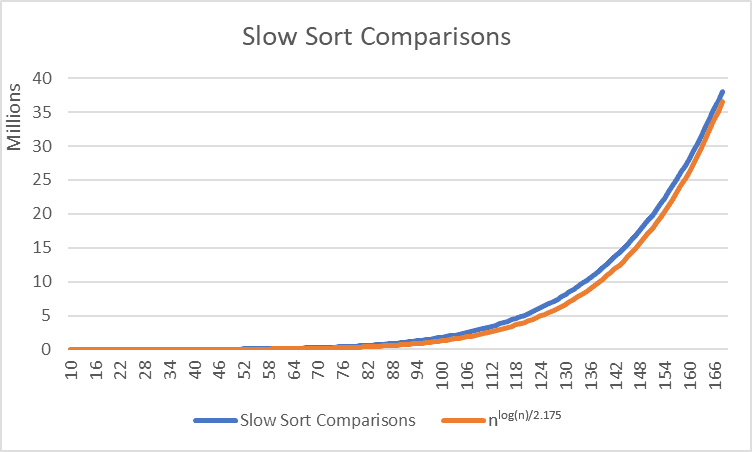
The time complexity for Slow Sort is the only one that I know whose comparisons grow exponentially as its list size n gets bigger. However, the exponent itself does grow very slowly so we do see this nice gradual curve instead of the instant spike that we got with a normal exponent like Hanoi Sort insertions.

Swaps

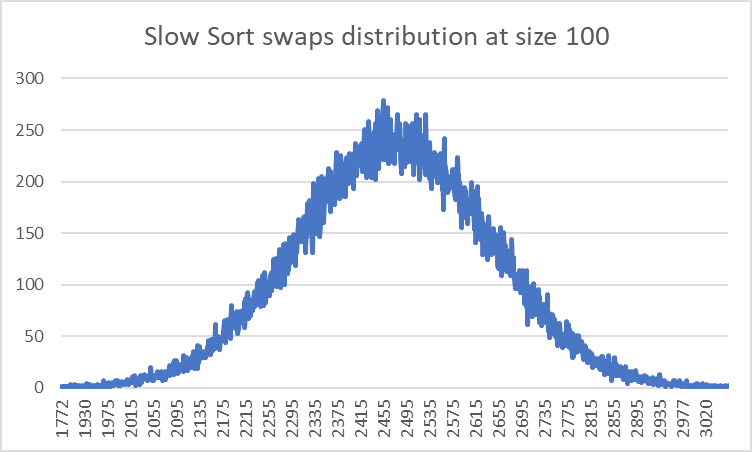
Swaps on the other hand are fairly standard. Since Slow Sort is very similar to Bubble Sort in how it places the highest item at the right one space at a time, it has an almost identical time complexity for sorts.

Distribution

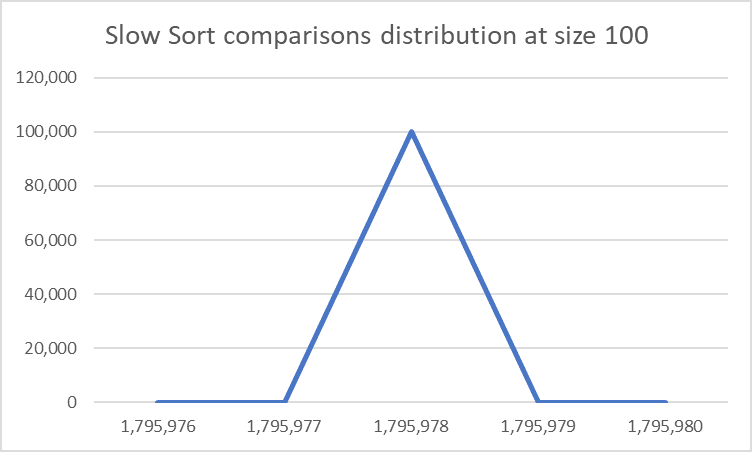
This is how the comparisons and swaps are distributed for this sorting algorithm of size 100 for 100,000 sorts.

Mode: 1,795,978
Mean: 1,795,978
Std dev: 0
Max: 1,795,978
Min: 1,795,978

Mode: 2,455
Mean: 2,474
Std dev: 167
Max: 3,184
Min: 1,772

Comparisons in Slow Sort are determined by number of items in the array to sort and not at all affected by the order in which they are in. This makes sense since it has some similarities with Bubble Sort (without the P).

C code

void slow_sort_recursive(int *p, int start, int end) {
	// Don't do anything if the length of array is 1
	if (end <= start) {
		return;
	}

	int mid;	// The midpoint of the array

	// Split the array in half
	mid = (start + end) / 2;
	slow_sort_recursive(p, start, mid);
	slow_sort_recursive(p, mid+1, end);

	// Do the check
	if (is_less_than_p(&p[end], &p[mid])) {
		swap(&p[end], &p[mid]);
	}

	// Do it again, without the final item in the list
	slow_sort_recursive(p, start, end-1);
}